Introduction.

String theory, also known by names such as "superstring theory" and sometimes "M-theory", is an idea that has been around for a rather long time, over two decades. It is, at one and the same time, a logical continuation of established theoretical notions dating back over half a century, and a radical new paradigm in fundamental physics.

Perhaps it is this paradoxical nature of String Theory that explains why it attracts so much attention today. Developments in this subject have hit the newspaper headlines more than once in recent years, and yet there is no direct experimental evidence that string theory is the fundamental theory of nature.

To appreciate what string theory aims to achieve and how it attempts to fulfill these aims, it is necessary to recollect the present formulation of the physics of elementary particles and fields. After reviewing the basic principles of particle physics, we will turn to a description of the fundamentals of string theory in non-technical terms.

Elementary Particles and Fields.

Consider the familiar force of electromagnetism. At the simplest level (applicable to many phenomena at everyday scales of distance) it is described by a "classical field". In this picture, a magnet exerts a force on another magnet because each one is a source of an electromagnetic field, pervading all of space but becoming weak with distance away from the source. The field needs no medium to support it, and can be thought of as a perturbation of the vacuum. Postulating the existence of such a field, subject to "wave equations", explains, in a unified way, all phenomena associated to electricity and magnetism up to a point.

The classical field theory of electromagnetism breaks down at very short distances, or in the presence of very strong fields. It becomes necessary to assume that this field is not just a number at every point of space and time, but a "quantum operator", having definite but somewhat complicated mathematical properties. The quantum field reduces to the classical one under familiar circumstances, but differs sharply from it in some regimes of distance or energy.

In quantum theory, a field is not just something associated with waves, but is also related to particles by virtue of the well-known wave-particle duality. An elementary particle is a sort of coherent excitation of a quantum field. Thus, the electromagnetic field must be associated to a fundamental particle occurring in nature. Indeed, such a particle exists and is called the "photon". An intuitive picture of an electromagnetic interaction, as described by quantum theory, is that the field quantum is exchanged between the objects that interact. Thus, a pair of magnets, when they approach each other, exchange photons, and it is this exchange that leads to the force between them. One may say that the existence of the photon is predicted by the very existence of quantum electromagnetic interactions.

Remarkably, all the interactions that are needed to explain chemistry (and, as far as we know, biology) are electromagnetic in nature. Atoms interact electromagnetically to form molecules and compounds. In a sense, therefore, we could claim that electromagnetism (which is correctly described by a quantum field theory) is a "unified theory of chemistry". This in no way reduces the importance of the chemist's research! Often, the underlying unified theory is not the most practical tool to answer the questions that a chemist wants to address. But it is still deeply satisfying to be assured that electromagnetism is the complete theory that in principle underlies and unifies all chemical phenomena. We will have more to say about the idea of unified theories in what follows.

Like electromagnetism, every other fundamental interaction must have its own mediating particle. Precisely three other kinds of fundamental interactions are known. One of these is the familiar force of gravitation, while the other two are nuclear forces that were only discovered in this century: the "strong nuclear" and the "weak nuclear" force. The former is, in particular, responsible for the binding of protons and neutrons to make up the nucleus of an atom, while the latter is a totally distinct force and gives rise to phenomena such as radioactive decay. The weak force is the only one which violates left-right symmetry or "parity". Gravitation, like electromagnetism, is a long-range force, which is why these two have been known for a long time. The two nuclear forces are short-ranged, and are therefore not commonly observed at everyday distance scales.

So, we may ask what is the elementary particle associated to each of these interactions. To gravitation, we associate the "graviton", a particle that has not been directly observed but is strongly believed to exist. To the strong nuclear force we associate a set of particles called "gluons" because of their glue-like binding properties, and to the weak nuclear force we associate another set of particles called "W and Z bosons". There is compelling evidence for the existence of gluons, while W and Z bosons produced at accelerators have been tracked directly. This, then is a summary of all fundamental forces and force-carriers known or believed to exist as of today (see Table 1).
 
 

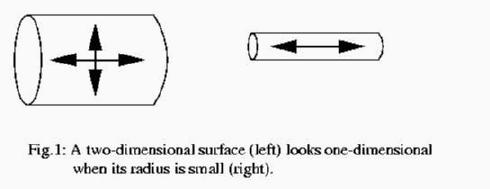
Clearly this is not the whole story of fundamental particles. Particles like electrons and neutrinos experience one or more of the forces described above, but are not themselves force carriers. They are thought of as "matter particles" (though photons and gluons are not really any less material). Matter particles are usually fermions -- particles with an intrinsic angular momentum (spin) that is half-integral in appropriate units. Force carriers like photons and gravitons are "bosons", particles that carry integer spin. In fact, all the force carriers except the graviton have spin 1 in units of Planck's constant, while the graviton has spin 2. This curious difference between the graviton and other force carriers is in a way responsible for the importance of string theory, as we will soon see.

Quantum field theory, then, is a mathematical framework to describe interactions among force carriers and matter particles. In its domain of applicability, it has been a stunning success. The scattering process that takes place when an electron collides with another, for example, can be described very accurately using this framework. We are dealing with something utterly basic, an interaction between indivisible particles due to a fundamental force that has no deeper origin as far as we know.

Some Difficulties Along The Way.

There are two problems with this story, one apparently aesthetic and the other apparently technical. But like all genuine difficulties encountered in the history of scientific research, these seem to point the way to a future that is a dramatically rich extension of the present.

The aesthetic difficulty is almost obvious even to the lay person. In a fundamental theory with no deeper explanation, why should there be such a profusion of fundamental forces and matter particles? Electrons, muons, neutrinos, quarks, W bosons, gluons, gravitons... the list is rather large and the whole collection of particles begins to look like a zoo. This is disturbing if these particles are supposed to be the ultimate constituents of matter.

The technical difficulty is harder to explain, but it is rooted in a simple fact. The mathematical description of spin-1 particles, while extremely intricate, is by now rather well-understood thanks to the ingenious work of physicists in the 1960's and 1970's. At the classical level, it started with Maxwell's famous equations for electromagnetism, and their generalization in 1954 due to Yang and Mills. (Together, all these theories are sometimes called "gauge theories"). The corresponding quantum theory was formulated for electromagnetism by Feynman, Schwinger and Tomonaga in the 1940's, and for the Yang-Mills generalization by 't Hooft and Veltman in the 1970's. (These were landmark achievements: Feynman et. al. received the Nobel Prize in 1965, while 't Hooft and Veltman were awarded the Nobel Prize in October 1999, even as the present article was being completed.)

Quantum electromagnetism describes the photon and its interactions with charged particles, while quantum Yang-Mills theory describes W and Z bosons and gluons (the carriers of weak and strong nuclear forces) and their interactions. The combination of all these theories makes up a single large theory called the "Standard Model" of particle interactions, which is a quantum gauge theory. Indeed, the Standard Model predicted the existence of the W and Z bosons before they were found. It also predicts a particle called the "Higgs boson" that is yet to be discovered.

The reader will have noticed that the Standard Model, as described above, does not include the graviton and its interactions. This is because the graviton, having spin 2, is not described by a gauge theory. In fact, we know what is the classical theory corresponding to the gravitational interaction: it is Einstein's legendary General Theory of Relativity. The technical difficulty is that we do not have a corresponding quantum theory. Despite our success with spin-1 particles (embodied in gauge theories), to date all attempts to formulate a quantum theory of spin-2 particles on the same lines have failed. If a fundamental theory of all interactions can be called a "theory of everything", then the Standard Model is a highly successful and experimentally tested theory of "three-fourth of everything" (since it incorporates three of the four fundamental interactions). While this is impressive, it means that the Standard Model is clearly not the final theory.

The reason why the Standard Model is useful despite the absence of gravity is that the strength of gravitational interactions depends on the masses of the gravitating bodies involved. For elementary particles, the gravitational force between them is so small that one cannot even conceive of observing it directly. Hence it is absent for all practical purposes, and our ignorance of a quantum theory of gravity does not stand in the way of verifying the Standard Model by comparison with experiment.

Nevertheless, without gravity the Standard Model is seriously incomplete. This is where string theory comes into the picture.

Three Attempts At Unification.

Before moving on to string theory, it is useful to recall three directions which grew out of the aesthetic dissatisfaction at having so many fundamental forces and particles.

The Kaluza-Klein Idea.

The first of these, dating back right to the beginning of this century, seems now to have been far ahead of its time, both in its analysis of the problem and the boldness of the solution. In the 1920's, the physicists Th. Kaluza and Oskar Klein independently observed that gravitation and electromagnetism (the only two fundamental forces known at the time!) were, in a sense, one too many. They felt it would be far more pleasing if both of these could be derived from a single common origin.

In the Kaluza-Klein proposal, space has extra dimensions beyond the three that are commonly observed. The simplest example is to assume four spatial dimensions altogether. However, one of these four dimensions is not infinitely extended, so that we can traverse it and experience it, but curled up on itself. It is rather like a walking-stick, on which a fat insect would be constrained to move only in one direction (along the length of the stick) and would not discover that the stick had a finite, but small, width constituting an independent dimension of its (two-dimensional) world (Figure 1).

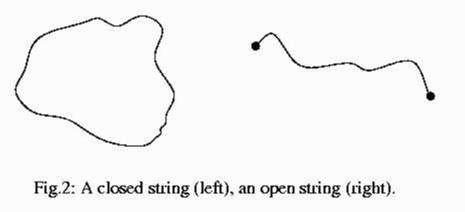
Kaluza and Klein then postulated that in this world of four spatial dimensions, there is only gravitation and no electromagnetism. A straightforward calculation reveals that when one of the four spatial dimensions is curled up, the spin-2 particle (graviton) in four spatial dimensions effectively splits up into both a spin-2 particle and a spin-1 particle in three space dimensions. Moreover, these particles satisfy the right equations to describe gravitation and electromagnetism in the physical world.

The Kaluza-Klein proposal, that one or more spatial directions are "compactified", remained a curiosity for several decades. Their proposal only provided a classical framework in which Einstein's gravity and Maxwell's electromagnetism had a common origin (this was hardly their fault, as quantum field theory had not yet been invented at the time!). The difficulty in implementing it seriously came from the fact that, despite attempts, no quantum theory could be associated with their idea. As we mentioned earlier, there was no known consistent quantum theory of gravity even in three spatial dimensions, and it turns out that in higher dimensions the difficulty in constructing such a theory is even more severe. However, as we will see, in the context of string theory this difficulty goes away, and both quantum gravity and higher spacetime dimensions are no longer impossible to deal with.

Grand Unification.

A different direction of research, initiated in the 1970's, was the proposal that at least the three fundamental forces associated to the Standard Model could be unified into a single force at high energy scales. This proposal, dubbed "Grand Unification", made use of the fact that the electromagnetic, weak and strong forces all seemed to arise from a common mathematical structure, the "Yang-Mills" theories. Could there be one such theory of which these three forces were merely different manifestations?

This proposal ignored gravity for the most part, so it was not as ambitious as the Kaluza-Klein approach, but it made some progress without radical assumptions like hidden spatial dimensions. It exploited a basic property of quantum field theories: their physical manifestation depends strongly on the energy scale of the particles involved. At very high energies, a theory may appear to describe one set of particles with one set of symmetries, while at low energies the particles and symmetries can change dramatically. In particular, symmetries which are present at a high energy scale can be "broken" at lower energies.

Thus, grand unification postulates that at high energies there is a single gauge force, mediated by a a family of fundamental particles. These particles would all be related to each other by the "gauge symmetry" that is manifested at these energies. As we come down in energy scale, this symmetry gets broken and the single gauge force splits into three distinct forces: the electromagnetic, the weak and the strong forces. Conversely, by going up in energy, the three forces (which have different strengths) tend to unify gradually, until at a particular scale they have the same strength and can be ascribed a common origin.

Indeed, a variant of this mechanism already operates in the Standard Model, where the electromagnetic and weak interactions are unified in this way. Above some energy, they combine into a single force called the "electro-weak" force. Grand unification extrapolates this idea, but the energy at which unification takes place is very high, over 10 orders of magnitude higher than the energies accessible at present-day accelerators.

Grand unification ran into difficulties too. Extrapolating a theory to very high energy scales poses a problem sometimes called the "hierarchy problem". This can be loosely stated as follows: if the various forces in a theory become unified at a very high energy scale, then this "natural" energy scale is much higher than the masses of familiar elementary particles such as electrons and quarks. In such a situation, one has to explain why these particles are so much lighter than the natural energy scale of the theory (as we mentioned, the discrepancy is by over ten orders of magnitude!). This problem may not seem very serious to an outsider, but practitioners of quantum field theory believe that an unnatural hierarchy of disparate energy scales in a theory is a sign of some serious inconsistency.

Supersymmetry.

A completely different direction of research which aimed at reducing the mysterious multiplicity of elementary particles, was the proposal in the early 1970's of a new symmetry called "supersymmetry". This is a mathematical transformation which related particles of integer spin (bosons) to particles of half-integer spin (fermions).

As we have seen above, bosons tend to be the mediators of fundamental forces, while fermions make up the "matter" which experiences these forces. With supersymmetry, it was hoped that bosons and fermions would, for the first time, be linked in a fundamental way. This would perhaps make it possible to start with a few fundamental forces and their associated particles, and then, assuming supersymmetry, to derive the existence of the remaining particles.

Unfortunately, by analyzing the mathematics, it became clear very soon that the known elementary particles were definitely not partners of each other under supersymmetry. Like Kaluza-Klein compactification and grand unification, supersymmetry too seemed to be a problematic idea.

As it turned out, rather surprisingly, supersymmetry turned from a failed idea to a potentially successful one when it was recogniszed that it could cure the deficiency of grand unification. Instead of assuming that supersymmetry relates known bosons and fermions to each other, one makes the (apparently wasteful) assumption that supersymmetry relates known bosons and fermions to presently unknown fermions and bosons! This right away doubles the number of particles in the zoo, and also requires us to explain why the "other half" have not yet been observed. And yet, there is a tremendous potential gain here.

Particles which are paired by supersymmetry must have the same mass. Since known particles do not occur in pairs of the same mass, supersymmetry must be "broken" at some energy scale. Above this energy scale, supersymmetry would be manifest but below that it would not. As a result, the "super-partners" would be observed only at accelerators operating above the energy scale at which supersymmetry is manifest.

By combining supersymmetry and grand unification, one can make a theory in which the breaking of the grand unification symmetry takes place as usual at very high energies, but the breaking of supersymmetry takes place at considerably lower energies, just above the energies at which present-day accelerators operate. In this situation it turns out that supersymmetry solves the "hierarchy problem": in supersymmetric unified theories of this sort, it is natural for some particles to be light even though the natural energy scale is very high. Thus, supersymmetry and grand unification co-exist better than each one separately.

There is a bonus: the unification of coupling constants at a high energy scale, that we discussed above, does not really take place without supersymmetry. There are three coupling strengths in the Standard Model (corresponding to the three forces that it unifies), and with present-day precision it has emerged that there is no single energy at which they all become equal. However, incorporating supersymmetry into the standard model changes the rate at which the couplings vary with energy. In the supersymmetric theory, couplings really do unify at a single point. This is a remarkable additional reason, independent of the hierarchy problem, for incorporating supersymmetry into a unified theory.

Today, even if one ignores string theory, the twin ideas of supersymmetry and grand unification are very much alive and are the subject of intense theoretical and experimental research. However, such models suffer from various limitations, and they do not include the fourth -- and most familiar -- force, gravitation.

The String Postulate.

A Theory of Strings.

The discovery of string theory as a potential unified theory was something of an accident. In a context unrelated to the unification of forces, researchers in the 1970's wondered what theory one might be able to write down to describe a fundamental quantum string -- an object with a finite spatial extent, which could not be described in terms of deeper constituents. It was certainly an interesting new mathematical problem in a physical context.

Such a string would be described classically by giving the location of an object extended like a (straight or curved) line in space at a given time. The string could be closed, like a loop, or open, with two end points (Figure 2).

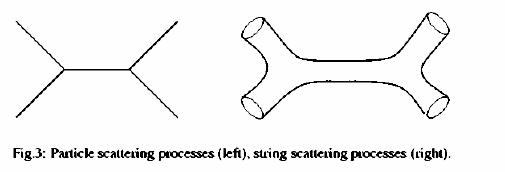
Just as a particle has an intrinsic mass, a string would have an intrinsic tension. Just as a particle is subject to the laws of special relativity, a string would also be relativistic. Finally, one would have to devise a "quantum mechanics" of strings in analogy with that for point particles.

The presence of an intrinsic tension means that string theory possesses an inherent mass scale, a fundamental parameter with the dimensions of mass. This defines the energy scale at which "stringy" effects (effects associated to the oscillation of the string) become important.

Without even doing a calculation, one can predict from experience that a quantum string should have infinitely many, discretely spaced oscillation modes, very much like the string of a musical instrument. All these modes would effectively be localised in the neighbourhood of the string, and would behave like elementary particles with different masses related to the oscillation frequency of the string. Thus a single species of string would produce lots of particle-like excitations. Could the zoo of elementary particles be explained in this way, as arising from a string?

The details ought to have been relatively straightforward, but several unexpected results emerged. A string is like a collection of infinitely many point particles, constrained to fit together to form a continuous object. Thus it effectively has infinitely many degrees of freedom -- always a dangerous thing! The mathematics of relativistic strings was fairly straightforward at the level of classical theory, but on attempting to promote it to a quantum theory, researchers discovered that the total number of spacetime dimensions is fixed uniquely to be 26. So, quantum strings could exist only in a world with 25 (rather than 3) spatial dimensions, plus time. The excitement of finding -- for the first time -- a mathematical consistency condition that determines the number of spacetime dimensions, rather than treating this number as an experimental input, was somewhat tempered by the absurd value predicted for this number.

Enthusiasm was further dampened by the discovery that even in 26 spacetime dimensions, the string has an additional unpleasant feature. Its spectrum of particle-like excitations includes one particle whose mass is an imaginary number -- a "tachyon", generally believed to be an unphysical object.

Never easily put off by such obstacles, theorists noticed that the theory held yet another surprise. After the tachyon, the next particle in the spectrum of the oscillating string was a spin-2 particle with vanishing mass. A massless particle can propagate to very large distances, so the force that it mediates is a long-range force. As we have seen, a spin-2 particle mediating a long-range force is just the missing ingredient in our search for a fundamental description of nature: the graviton. We learned that previous attempts to incorporate the graviton failed for technical reasons associated with quantum field theory. Was the theory of strings powerful enough to overcome these obstacles?

Here lay the principal breakthrough due to which string theory has become as important as it is today. The very nature of strings -- that they are extended, and not pointlike -- turns out to cure the inconsistencies that had always plagued quantum theories of gravitation. While the diagrams describing the scattering of point particles have definite points where a particle splits into two particles, the corresponding diagrams for string scattering are completely smooth (Figure 3). This simple fact is ultimately responsible for removing the singularities in the process of graviton scattering which made quantum gravity inconsistent and for which no cure had been found. Thus, despite 26 dimensions and the unphysical "tachyon" particle, string theory was found to contain a promising solution to the problem of gravity.
 

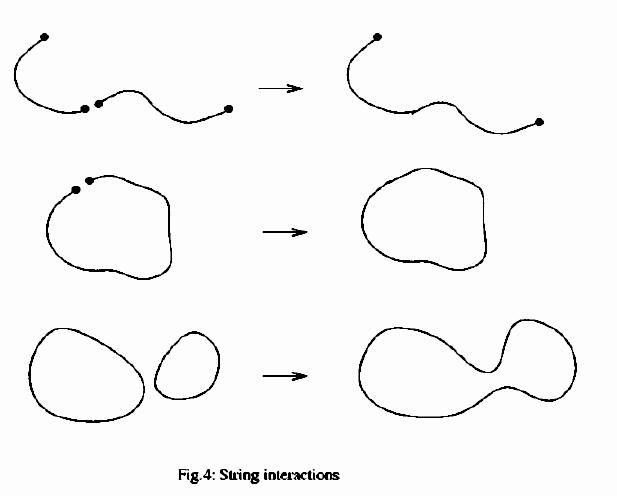
Superstring Theory.

This promise became more convincing when a better string theory was found which had no tachyon, and which did not require as many as 26 spacetime dimensions, but which retained the massless graviton-like particle. Remarkably, this tied together all the ideas that we encountered in the preceding sections: supersymmetry, unification and the Kaluza-Klein proposal.

In string theory, the tachyon arose as an excitation having negative mass-squared. From the point of view of an observer on the string itself, this excitation appeared as a state of negative energy. This was connected to a familiar fact in quantum mechanics: because of the famous uncertainty principle, the minimum energy of a localised system tends to be non-vanishing. The presence of a tachyon in string theory could be mathematically traced to the presence of this non-vanishing "zero-point energy" in typical quantum systems. It followed that if we could identify special quantum systems where the zero-point energy vanished, we would possibly be able to invent a special string without any tachyon.

Quantum systems without a zero-point energy occur in the presence of supersymmetry. We mentioned earlier that this symmetry relates bosonic and fermionic degrees of freedom. The zero-point energies associated with these two types of degrees of freedom turn out to be opposite in sign, and cancel out identically in a supersymmetric system. Although the historical route to this discovery was somewhat more complicated, our modern understanding is that this is the key to a string theory which has no tachyon -- "superstring theory".

Going from string to superstring theory finally led to a proposal which seemed well-suited to describing the real world, or at least better-suited than many previous proposals. In superstring theory, the basic postulate is, as before, that vibrations of a single type of string lead to a multitude of elementary particles. But because of supersymmetry, there is no tachyon. As a bonus, the consistency condition on the number of spacetime dimensions changes when supersymmetry is introduced. Thus, instead of 26, superstring theory requires just 10 spacetime dimensions. Finally, the presence of a "graviton" particle is maintained in superstring theory, so it is still a theory of gravity -- in fact, of "supergravity", the supersymmetric extension of gravity.

Properties of Superstring Theory.

The fundamental object in superstring theory is the superstring: a string with extra degrees of freedom that make it supersymmetric. After the long chain of developments that we have discussed, that led to the formulation of this theory, it is time to discuss the theory and its relevance to the real world in some detail.

Five Different Theories.

A string can be either open, with two end-points, or closed, like a loop. The natural physical postulate for interactions between two open strings is that when their end-points touch, they join together into a longer open string. However, if the two end-points of a single open string touch, they can join together and make a closed string. Thus, theories of open strings inevitably contain closed strings as well (Figure 4).

The reverse is not true. A pair of closed strings can join when any pair of points coincides, to make a single closed string. Thus there can be theories with only closed strings and no open strings. It turns out that the most natural prescription leads to a single possible open string theory, called type I superstring theory, and two distinct closed string theories, called type IIA and type IIB string theory. A clever hybrid of the superstring with ordinary (non-supersymmetric) string theory, called the "heterotic" string, was also discovered and there are two such theories, making five altogether. Nowadays we have a better understanding of why these are the only five superstring theories and how the five are mutually inter-related.

The lightest excitations of a string theory can be described by a quantum field theory with a certain number of elementary particles, so we will describe the content of this field theory, temporarily ignoring the fact that there are infinitely many string excitations of increasing energy. For the open string, the low-energy theory is a field theory in 10 spacetime dimensions with a (massless) graviton and a collection of "gauge" fields very much like the fields describing photons, W and Z bosons and gluons in the real world. Thus, interactions of the type found in nature (gravity and gauge forces) are incorporated in type I superstring theory, albeit in 10 dimensions. Fermionic matter particles are present too. They are charged under the gauge interactions, analogous to the fact that electrons have electric charge or that quarks carry a "colour charge". Also, the fermions are of a definite "handedness" or "chirality", which means that type I theory in 10 dimensions violates parity or left-right symmetry, just as the weak interactions do in the real world. This is extremely encouraging, because all these particles and interactions follow from the simple postulate of a consistent open superstring theory!

There are several obvious negative points too. The symmetry group associated to the gauge particles of the type I string in 10 dimensions is SO(32), much larger than the expected symmetry group of the strong, weak and electromagnetic interactions in the real world, which is the product of SU(3), SU(2) and U(1). So we seem to have too many forces and their corresponding carriers. Also, all the particles appearing in the low-energy theory are exactly massless, quite different from the real-world electron or quark which has a definite mass. Finally, we are in the wrong number of spacetime dimensions -- 10 rather than 4. But none of these is a genuine obstacle. At extremely high energies, for all we know the real world might well look 10-dimensional and have lots of nearly massless particles and a very large gauge symmetry group. So one should treat 10-dimensional superstring theory in this light -- as a candidate description of the high-energy limit of the real world. To connect this to the low-energy world we have to face issues like compactification to 4 dimensions and symmetry breaking.

The superstring theories of type IIA and IIB are somewhat different. They contain a massless graviton, but do not have the "gauge" type particles that are present in type I string theory. There are fermionic matter particles, but in the absence of force carriers of the usual type, these cannot carry charges. The fermions are parity-conserving in type IIA theory and parity-violating in type IIB. Finally, there are some exotic fields called "tensor gauge fields", which are roughly like higher-spin analogues of the photon. However, the fermions and other massless particles are not charged with respect to these. All of this was initially perceived as discouraging and these theories were for many years regarded as exotic and irrelevant to the goal of finding a unified theory of nature. Recent developments have shown this view to be false. The process of compactification can actually produce gauge particles and fermions charged under the gauge interactions. This is one consequence of the duality symmetries that will be discussed in the other articles of this collection.

Finally, let us describe the hybrid "heterotic" string. This was based on the observation that excitations of a closed string look like little waves which travel one way or the opposite way around the string. These two types of waves (called "left-movers" and "right-movers" for obvious reasons) do not interact with each other even though they propagate on the same string. Hence it is meaningful to combine ordinary left-moving waves with supersymmetric right-moving waves (rather than have both types of waves be supersymmetric, as in the type II strings). The heterotic string is based on this idea.

There is a puzzle right away: we saw that ordinary strings are consistent in 26 dimensions while superstrings live in 10 dimensions. How can these two be matched and in how many dimensions does the resulting theory live? The answer comes from an adaptation of the Kaluza-Klein idea. We take 16 of the 26 dimensions to be curled up on little circles. Then the resulting 10 dimensional theory is combined into the hybrid theory described above. So the final theory is 10-dimensional, but its left-moving waves have a 26-dimensional origin, and hence there are hidden degrees of freedom corresponding to the 16 extra dimensions. Remarkably, these hidden degrees of freedom are manifested as gauge fields, and the symmetry group depends on the sizes of these compact dimensions and the shape of the "torus" formed by the 16 compact dimensions. It turns out that consistency of the resulting string theory allows only two choices for this torus. One choice leads to a gauge symmetry group of SO(32), so the resulting theory closely resembles type I (open) superstring theory. The other choice leads to something quite new: the gauge symmetry group is a product of the exceptional group E(8) with itself. This is called the E(8) x E(8) heterotic string. It is the fifth and last superstring theory in 10 dimensions. 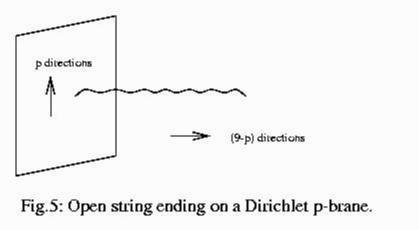Like the type I string, both the heterotic string theories are parity-violating in 10 dimensions.
 

Initial attempts to compactify these five string theories to 4 dimensions strongly favoured the E(8) x E(8) heterotic string. With the SO(32) strings (heterotic and type I) the parity violating nature in 10 dimensions appeared to be destroyed by compactification, so the resulting 4-dimensional theory could not describe the real world, which is parity-violating. This was also true of the type IIB string. On the other hand, the type IIA theory is already parity-conserving in 10 dimensions, and from what was known about compactification until recently, it apparently could not induce parity-violation. The modern picture is considerably different. All the five string theories are actually connected to each other, so in some sense they are all different limits of a single theory. This single theory is still not extremely well-understood, but it can lead to parity violation in 4 dimensions. Thus, which string theory one compactifies may depend on one's convenience: effects that are difficult to study in one formulation are often easier in the dual theory.

The Dilaton.

A few additional properties of superstring theories merit discussion. One of them concerns the question of the coupling constant of the theory. Quantum field theories usually contain an adjustable parameter which determines the strength of interactions. Actually, as we saw in a previous section, this parameter depends on the energy scale at which the interactions take place. It can be small at some energies and large at others, for example in the theory of strong interactions the parameter is large at low energies, leading to permanent confinement of quarks inside particles like protons and neutrons, while it is weak at high energies, leading to a picture of protons and neutrons as being made up of almost non-interacting quarks. This "flow" of the coupling with energy scale is characteristic of most quantum field theories where infinities occur in the computation of scattering amplitudes. However, superstring theory is free of such infinities because of the extended nature of strings. Thus one would expect string theory to contain a coupling constant that is a fixed number which we must determine by comparison with experiment.

What happens in practice is somewhat different. Instead of a coupling constant, all string theories have a scalar particle which governs the strength of the interactions. Technically, the field associated to this particle can take a definite constant value in a given "vacuum" of the theory, and that value acts like the coupling constant. This is a beautiful property because it suggests that the strength of string interactions could in some way be self-consistently determined by the theory instead of being an experimental input. This could potentially answer a deep question often posed by Dirac and others: in electrodynamics, why does the quantum of electric charge have the value, approximately equal to the square root of 1/137, that one finds from experiment?

At our present level of understanding, although we know that the dilaton is present in all string theories and that it determines the interaction strength, we still do not know how to determine the value that the field takes in the vacuum. Indeed, because of supersymmetry, the value seems undetermined and can be anything we like, which is almost like having a free numerical parameter in the theory. However, at low energies we expect supersymmetry to be broken. In this situation the vacuum value of the dilaton might get determined. Understanding this is one of the goals that string theorists hope to attain in the future.

Tensor Gauge Fields.

We mentioned that the type II string theories have exotic "tensor gauge fields" whose role was for a long time mysterious. Although the role of such fields will not be elucidated in the present article, it is important in order to understand string duality. Here we will focus on one particular tensor field which is actually present -- though we have not mentioned it so far -- in all the five string theories. This is the so-called "second-rank tensor field", which is like a photon but with one extra vector index under Lorentz transformations. Under Lorentz transformations, the photon (denoted A) transforms as a vector, unlike the tensor field (denoted B) that is ubiquitous in string theory, which transforms as the product of two vectors, hence is called a "second-rank tensor". The question we want to ask is rather simple: just as a point particle (such as the electron) can be charged under the photon field, is there some dynamical object in string theory that is "charged" under B? This is important, because such a charge can help to endow an object with stability. In real life, electrons are stable because they carry the minimum unit of electric charge and are the lightest such charged objects. Because of charge conservation, there is therefore nothing that they can decay into! Because B is present in all string theories, one may suspect that it too endows some suitable charged dynamical object with this property of stability.

The answer turns out to be beautifully simple: objects carrying charge under second-rank tensor fields are strings. Indeed, in all the closed string theories (type IIA, IIB and the two heterotic strings) the fundamental string carries unit charge under B and is therefore guaranteed to be stable.

The argument leading to this conclusion is fairly simple. In quantum mechanics, a charged particle has a coupling term eA integrated along the trajectory (called "world-line" in relativistic theories) of the particle. Here, e is the quantum of electric charge, and can be chosen to be 1 in suitable units. In closed string theory, one finds that the fundamental string has an analogous interaction consisting of B integrated over its trajectory, which is two-dimensional because the string itself has a spatial extent and propagates in time. This interaction tells us that the fundamental string carries unit charge under this tensor gauge field and is therefore stable. The situation is more subtle for open-string theories, so we will not address it here.

Open-string boundary conditions.

The final property of 10-dimensional string theory that we want to discuss here is that of boundary conditions on open strings. Unlike closed strings, open strings have endpoints, and this means that in defining the configuration space of the string, we have to specify the boundary conditions on these endpoints. The most natural choice would be to allow these endpoints to be located anywhere in space. Indeed, this is the only choice compatible with translation invariance and Lorentz invariance in 10 dimensions. If we "anchored" the endpoints in any way, it would distinguish some of the 9 spatial dimensions from the others. Mathematically, the boundary conditions that allow the endpoint of the string to be located anywhere in space, and hence satisfy Lorentz invariance, are called "Neumann" boundary conditions, familiar from the study of differential equations on spaces with boundaries. The alternative "Dirichlet" boundary conditions, which constrain the string endpoints to lie on definite surfaces in space, are clearly incompatible with translation and Lorentz invariance, and may preserve at most a part of these invariances.

However, Neumann boundary conditions (which for a long time were considered to be the only reasonable ones for open strings) turn out to be too restrictive and miss some very profound dynamical phenomena in string theory. The reason is as follows. Consider an ordinary quantum field theory of pointlike particles. Although the underlying theory has translation invariance and Lorentz invariance, the individual states of the theory do not. For example, while the vacuum state of such a theory is translation invariant, the theory also has one-particle and multi-particle states in its spectrum. These states involve particles located at fixed positions (for example, imagine the state of a single particle at rest at a definite point). It is no surprise that this state breaks translation invariance.

One may therefore imagine that if we assign boundary conditions to open strings that violate translation and Lorentz invariance, we get a definite state of the theory, different from the vacuum state. This turns out to be true, and has a variety of deep and beautiful consequences. Suppose as a first example, we assign Dirichlet boundary conditions to the endpoints of an open string, along all the 9 spatial coordinates (x1,x2,...,x9). This constrains the endpoint of the string to lie at single position in space, while the rest of the string is free to fluctuate. For example, we can constrain the end point to lie at the origin in some coordinate system. Then this point becomes "special", and indeed behaves like a pointlike particle. For example, it breaks translation and Lorentz invariances in exactly the same way that a point particle state in a 10-dimensional field theory would. But this state is not one of the point particle-like excitations of the closed string that we have discussed! Quite the opposite -- it is an object defined by the property that open strings terminate on it. It turns out that one can assign a definite mass and charge to such an object, and that it behaves just like an elementary particle. It is commonly termed a "D-particle", where the "D" is a reminder that it arises by assigning Dirichlet boundary conditions to the endpoints of open strings.

So far we discussed two possible boundary conditions: Neumann in all 9 directions, or Dirichlet in all 9 dimensions. We can easily postulate a hybrid of the two, say Neumann in 2 directions and Dirichlet in the other 7. This corresponds to an open string that is "nailed" onto a two-dimensional spatial surface. Then, just as for the D-particle, we will be forced to interpret this entire surface as a dynamical object that extends in 2 spatial directions, commonly known as a "membrane". Therefore, just by assigning such boundary conditions, we have produced a quantum state of string theory that is extended in space like a membrane. It is a different issue whether this membrane is stable. It will be so if it is charged under some generalised gauge field, just as the string was stable because of its charge under the second-rank tensor field. Indeed, it is straightforward to see that a membrane can be charged under a third-rank tensor field, just because the trajectory of a membrane is a three-dimensional surface in spacetime. This happens in type IIA string theory, where indeed the spectrum contains a third-rank tensor field. Hence type IIA string theory is not just a theory of particles and strings, but also membranes.

This is easily generalised. If we assign p Neumann and 9-p Dirichlet boundary conditions, the correspond state is extended in p spatial directions and is called a "Dirichlet p-brane", or Dp-brane for short (Figure 5).

Such an object may be hard to visualise in our cramped world with only 3 spatial dimensions, but they have plenty of room to propagate in 9 spatial dimensions! Thus we see that string theories are not just theories of strings. They contain, in a very natural way, extended objects called branes in their spectrum. Note that among other things, D-branes provide an explanation of the role of the exotic tensor gauge fields in type II string theories: they endow the branes with stability.

In the study of string theory, branes turn out to be just as important as strings -- in fact, one may say that fundamental strings are only a special type of p-brane with p=1. One should be careful, though, to realise that the fundamental string is not a Dirichlet brane as we have defined it. It is postulated from the beginning, and not defined in terms of something else ending on it. The Dirichlet branes are special precisely because they are defined through fundamental strings that end on them. This enables us to study them using familiar techniques of string perturbation theory.

Compactification.

Finally, we turn to the relationship between the 10-dimensional world described above, (with 9 spatial and 1 time dimension) and the real 4-dimensional world (3 spatial and 1 time dimension) that we inhabit. The key requirement is that the 9 spatial dimensions that we start with should not all be physically observable. In the spirit of Kaluza and Klein, we therefore assume that 6 spatial dimensions are "curled up" on themselves, while the remaining 3 dimensions extend to infinity (or at least to very large distances). The concept of "space" is embodied in mathematics by the notion of a "manifold", something that locally looks like familiar space but may have curvature and other nontrivial properties. In particular, a manifold that is "curled up" in the way that we desire is called "compact". Thus, the most straightforward way to connect string theory to the real world is to postulate that 6 spatial dimensions form a compact manifold, whose size is so small that we are unable to detect its existence directly with the probes available to us.

Theoretical investigations of this compactification scenario have revealed a rich connection with the branch of mathematics known as Algebraic Geometry. The connection seems to have been helpful in both directions -- while known results in mathematics helped to gain an understanding of the manifolds that may be potentially relevant to string theory, the string-theoretic setting also proved helpful to extract new mathematical results (we will not have the time to go into the latter aspect here). A class of 6-dimensional manifolds with very special properties, known as Calabi-Yau manifolds, turn out to have properties which -- when they are used as the compactification manifolds in string theory -- lead to tantalizingly realistic theories in 4 spacetime dimensions. The detailed particle content and dynamics of the 4-dimensional theory depend on the choice of Calabi-Yau manifold, so it is not as if the manifold is completely unobservable. In fact, this way we get to have our cake and eat it too -- the Calabi-Yau manifold would be responsible for the "zoo" of elementary particles observed in the real world, but it would not be directly observable as a collection of extra spatial dimensions -- a good thing since such extra dimensions have not been observed, at least so far.

Initially, the most realistic class of theories was found by starting with the E(8) x E(8) heterotic string in 10 dimensions and compactifying it on a suitable Calabi-Yau manifold. For example, in this way one is able to recover 4-dimensional theories with gauge groups large enough to include the SU(3), SU(2) and U(1) groups associated to the standard model (and not too much more, which would lead to unobserved additional interactions). The 4-dimensional theory is parity-violating, because the underlying heterotic string is parity violating and the compactification process in this case does not wipe out parity violation. Besides the gauge particles, there are matter particles (fermions) which qualitatively have the right sort of "quantum numbers" to be identified with the known fermions in nature, such as electrons, muons, neutrinos, quarks etc. And of course there is gravity in 4 dimensions, because string theories describe gravity in 10 dimensions and compactification does not destroy this property.

At a very rough level, this is rather convincing evidence that we are on the right track. However, a variety of problems remain. For example, for reasons associated with the hierarchy problem endemic in grand unification, the compactifications that are favoured give rise to a supersymmetric theory in 4 dimensions. But this still leaves open the question of how and why supersymmetry breaks at lower energies to give rise to the apparently non-supersymmetric world in which we live. Also, the lightest elementary particles arising from string oscillations are in fact exactly massless in 10 dimensions, and they give rise to a multitude of exactly massless particles in 4 dimensions after compactification. This contrasts unfavourably with reality -- the only exactly massless particles in the world, so far as we know, are the photon and the graviton. The real-world electron has a nonzero mass, while the string-derived electron (though it has appropriate charges and other quantum numbers) is apparently massless. It is believed that masses for these particles will appear once supersymmetry is broken, but the details of that process are far from understood.

While compactification as outlined above remains an important mechanism to extract real-world physics from string theory, it is remarkable that several other mechanisms have been proposed just in the last three or four years, on how to extract the content of the standard model from string theory. Some of these new ideas claim to overcome the hierarchy problem and other problems associated to the conventional compactification approach sketched above. However, it the dust has yet to settle on these competing claims, and so the present is not the most appropriate time to review these new ideas. In another two or three years it should be much clearer whether there is a detailed, consistent and tractable scenario to connect string theory to the real world.

A closely related problem in relating string theory to nature is the problem of the "cosmological constant". The theory of gravity admits a parameter that roughly describes the total energy of the vacuum. The presence of such a parameter would have dramatic observable consequences and would affect the rate of expansion of the universe. This enables us to put a very stringent bound on the actual value of the parameter from experiment. As a fundamental theory of gravity, string theory should predict the value of this parameter -- but instead, it tells us something quite unsatisfactory about it.

In superstring theory, as long as supersymmetry is unbroken, the cosmological constant is identically zero due to cancelling contributions from bosons and fermions. This has long been thought to be consistent with experiment (recently it has been suggested that in fact the parameter has to be nonzero but extremely small). But the problem is that supersymmetry is broken in the real world, and after supersymmetry breaking the cosmological constant generically takes a nonzero and extremely large value -- roughly 100 orders of magnitude larger than the experimental bound! This is another hierarchy problem. The problem is not specific to string theory, but rather, it is in string theory, as the first serious candidate for a quantum theory of gravity, that we have the right to expect a solution -- and this has not yet been forthcoming, though again there is an abundance of new ideas in recent years.

Concluding Remarks.

This has been a qualititative survey of some elementary features of string theory. The focus has been largely on properties that have been known for over a decade, and which together are described as "perturbative string theory". However, since 1994, major advances in nonperturbative string theory have taken place.

Nonperturbative physics is the study of physical effects which cannot be described order-by-order in terms of a small coupling constant. A typical nonperturbative effect is the binding of two particles, for example an electron and a positron, to form a new particle -- in this case, positronium. For zero interaction strength there will be no binding, which is physically very different from the true behaviour where binding is possible. This means, as should be quite obvious, that one cannot approximate a bound state in terms of unbound particles. Absence of knowledge about nonperturbative effects in a physical theory means that the theory, even if correct, is seriously incomplete and cannot be used to study important phenomena which it is intended to describe.

With the present formulation of string theory (as compared with quantum field theory) this has indeed been the case. Although we have not overcome this serious incompleteness, a rather novel approach to string theory has helped us make major inroads into nonperturbative territory. The key technique has been to use internal consistency and selected computations as "evidence" to assess the truth of certain conjectures about the nonperturbative structure. This approach has uncovered the role of new symmetries called "dualities" in string theory.

Bibliography.

For an introductory article such as this, it is appropriate to cite only a few key textbooks rather than the original research papers. The lay reader will benefit from the introductory chapters in these books, while the more advanced reader will find a comprehensive list of technical references therein.

1. "Superstring Theory", M.B. Green, J.H. Schwarz and E. Witten, Cambridge University Press (1987).

2. "String Theory", J. Polchinski, Cambridge University Press (1998).

3. "Gauge Fields and Strings", A. M. Polyakov, Harwood Academic, 1987.

4. "Lectures on String Theory", D. Lust and S. Theisen, Springer-Verlag, 1989 (Lecture Notes in Physics, 346).

5. "Introduction to Superstring Theory", E. Kiritsis, Leuven Univ. Press, 1998 (Leuven Notes in Mathematical and Theoretical Physics, Vol. 9).

October 1999