Kakuro Navigation

Kakuro

Kakuro is a puzzle given on a grid of red and white cells. The digits 1 to 9 must be filled into all the white cells so that they satisfy the clues given in some of the red cells. The clues specify the sum of the numbers in the row of successive white cells to the right or the column of successive white cells below. No row or column of successive white cells can have a digit repeated. In other words, we can write 4=1+3 but not 4=2+2.

Technorati tag:

Related topic: Su Doku

Digg this

Add to del.icio.us

Kapenta

Kapenta: the old saws

(2)3=1+2
 4=1+3
 5=1+4=2+3
 6=2+4
 7=3+4
(3)6=1+2+3
 7=1+2+4
 8=1+3+4
 9=2+3+4
(4)10=1+2+3+4

Kapenta has the same rules as Kakuro except that the only digits allowed are 1, 2, 3 and 4. Since the second rule allows no repeats, this means that no clue can be longer than 4. All possible clues are given in this table. There is only one clue with a non-unique partition. We will write 62 and 72 when these two numbers are used in a clue for 2 white cells, but 63 and 73 otherwise.

When A and B are two clues which uniquely determine the number at their intersection, we write A∩B for that unique number (a∩B=B∩A). Among all 15 intersecting clues that could be placed in a 2×2 block, only the following 3 exist: 3∩4=1, 3∩62=2 and 4∩72=3. One also has 8 others: 3∩8=1=4∩73, 3∩9=2=62∩63, 4∩9=3=72∩63 and 62∩8=4=72∩73. The following 2 have no solutions: 3∩72 and 4∩62,. Everything else has multiple solutions.

The simplest templates: M=3,4

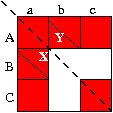
The counting for the template with M=3 has already been done. There are 3 essentially different solutions, labelled by the clues (3,4), (3,62) and (4,72). Under a reflection in the dotted diagonal, each generates another puzzle by interchanging the clues. There are 3 essentially different puzzles with M=3, each doubled if we count symmetry related puzzles separately.

These M=3 puzzles can each be extended to M=4 in two ways because [Cc] can be filled in two ways: either [Cc]=[Bb], or [Cc] is the fourth different digit. Clearly, therefore, M=4 puzzles are labelled by 3 clues (W,X,Y). There are 6 essentially different puzzles, each doubled under symmetries.

The templates M=5,6 inside 2×3 blocks

For every unique solution with M=4 inside 2×2 blocks, one can extend one of the rows or columns by one cell. Then there are two ways to fill this new cell, implying that the corresponding clue can be one out fo two. Therefore, there are 12 essentially different puzzles on this template, each doubled under interchange of the two equivalent rows or columns.

The rectangular 2×3 block allows unique solutions for Kapenta, unlike for Kaquadro. First, the two long clues cannot be the same, and no two of the three short clues can be the same, otherwise a permutation of any solution also yields a solution. To find all the solutions, start from the M=5 template analyzed above. There are two cases. In one case, the 5th cell value was different from either of the values in the parallel smaller clue. In this case, the new white cell added to that can be filled in exactly one way, since it cannot have any of the two values in one direction and one value in the other direction. In the second case, the new cell could have one of two values.

M=6,7 inside a 3×3 block

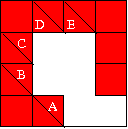
Carrying on the counting from the M=5 case, the new square can be filled in any of 3 ways. Hence there are 24 essentially different puzzles, each doubled under symmetry. The puzzles are labelled by the clues (A,B,C,D).

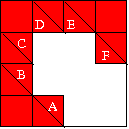
So here is the counting for M=7. Bb can be filled in 3 different ways. Each filling determines [Bc] and [Cb], and they are different. Now [Cc] can be filled in 2 different ways: [Cc]=[Bb] and [Cc]≠[Bb]. For each choice of [Cc], there are 2 ways of filling each of Cd and Dc. Of these exactly half have [Cd]≠[Dc], so [Dd] can be filled in either of 2 ways. The remainder can be filled in either of 3 ways. Therefore there are a total of 60 solutions, which lie in 30 essentially different classes. Each puzzle can be uniquely labelled by the clues (A,B,C,D,E).

The distinction between Kaquadro and Kapenta on this template is crucial. In Kaquadro, solving [Bb] gave an unique filling of the template. In Kapenta one needs to solve [Bb] and [Cc] independently. Extensions of this template to L intersecting 2×2 blocks, giving M=3L+1 has similar properties. In Kaquadro all such blocks were fixed as soon as [Bb] was solved. In Kapenta (and its larger siblings), these require solution of L free variables.

© Sourendu Gupta. Mail me if you want to reproduce any part of this page. My mailing address is a simple (satisfactory) puzzle for you to solve. Created on 30 November, 2006. Last modified on 4 December, 2006.