Tridib Sadhu
Reader at Tata Institute of Fundamental Research, Mumbai.
I am a member of the Condensed Matter and Statistical Physics Group of the Department of Theoretical Physics in Tata Institute of Fundamental Research, Mumbai campus. I am also an associate of the International Centre for Theoretical Sciences, Bengaluru.
My work is broadly in the area of out-of-equilibrium statistical Physics and stochastic processes. I am actively involved in an experiment-theory collaboration with Shankar Ghosh in the Soft Matter Laboratory in TIFR-Mumbai campus. For details see Research tab.
I am looking for prospective PhD students and Postdocs to work on related topics. Interested persons could contact me directly for possible projects.
Research.
Some of the research directions I have been working in recent times.
A theory for systems outside equilibrium.
For systems in equilibrium, statistical mechanics provides a systematic theoretical tool to relate thermodynamic properties to microscopic degrees of freedom. This is one of the great achievements of theoretical Physics from the last century. It gave us entropy as a measure of microscopic disorder, gave earliest evidence of atomistic world, the concept of universality and renormalization group emerged from studies of equilibrium phase transitions.
Current challenge is to find a similar general framework for systems outside equilibrium. Infact, non-equilibrium systems are more common in nature than systems in equilibrium. They are systems still evolving towards an equilibrium state (glasses, coarsening), or systems coupled at boundary with unequal baths (energy flow between two reservoirs, transport in quantum circuits), or microscopic constituents with an internal energy source (living matter, active particles).

Glasses are approaching equilibrium, but extremely slowly. Image taken from Physics today

Flocks of birds are examples of bulk driven non-equilibrium systems. Image source: nature journal. See this remarkable video of collective motion of bird flocks.
From existing works it seems unlikely that a general microscopic measure analogous to Boltzman-Gibbs formula extends outside equilibrium. However, in the spirit of Landau theory, a general mesoscopic description is likely, whose mathematical foundation lies in the theory of large deviations al la S R S Varadhan. See these two [1, 2] beautiful articles by Bernard Derrida and Hugo Touchette.
Questions that we try to address are, for example, what are thermodynamic state variables (like, pressure, temperature) for a non-equilibrium macro-state; are there state functions (like, free energy) that characterize macroscopic fluctuations and non- equilibrium phase transitions; is there universality outside equilibrium and can they be described by renormalization group; what are underlying constraints, symmetries in a microscopic dynamics responsible for non-equilibrium characteristics?
Our approach to these questions are following computer simulations of rare fluctuations, rigorous mathematical analysis of model systems using integrability techniques (Bethe ansatz, matrix product representation), and field theoretic approaches for hydrodynamic fluctuations (Macroscopic fluctuation theory). What binds all three approaches together is the concept of universality, making only certain underlying properties relevant for macroscopic behaviour.
For an introduction to these ideas you can see some of these beautiful lectures from the leaders in this subject.
Non-Markovian stochastic processes.
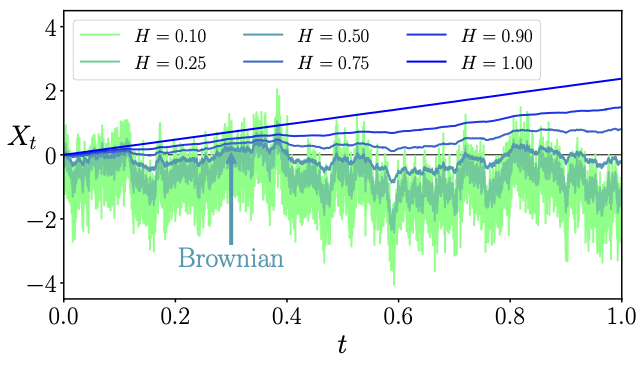
fBm trajectories for different Hurst exponents.
Brownian motion describes diffusive behavior in stochastic time series with finite auto-correlation. However, there are abundant natural examples that do not show a diffusive behavior, rather exhibit long-range correlations in time, leading to super/sub diffusion. Examples range from anomalous transport, solar flare activities, water levels in rivers, to price of stocks in financial markets.
The fundamental process that describes such a time series is due to Mandelbrot and Kolmogorov, and termed as fractional Brownian motion (fBm). Being non-Markovian, it is extremely hard to theoreticaly analyze such process, even their efficient numerical simulation is non-trivial. We use field theoretical tools and devise fast computer algorithms to analyze statistical properties of fBm. Broadly, our interest is in finding generalizations of well-known results of standard Brownian motion for an fBm, e.g., first passage time, arcsine-laws, law of iterated logarithms, passage through barriers, etc.
Pattern formation and self organized criticality.

Growing pattern in an Abelian sandpile model. (Abelian Sandpile is an incredible work of Deepak Dhar).
Eventhough basic physics laws are simple, how come our world around of us is complex? How does complexity arise from simple laws[see a chapter from my thesis]? A stiking example of such emergent complexity is life itself. How does a single fertilized egg develope into a multicellular organism with highly complex internal structures [the puzzling problem of proportionate growth]?
As a Physicist our interest is in understanding the underlying basic principles behind such emergent complexity. The picture on the left illustrates such complex pattern formation from simple local rules.
We want to understand the mathematics behind formation of such complex patterns. Structures in these simple models have interesting connection with discrete holomorphic functions, tropical polynomials, identity element of Abelian sandpile group, and Apollonian circle packing problem.
You can see more examples of such patterns here created by Wesley Pegden and a lucid introdution to the subject here by Jordan Ellenberg.
Area-law and universal logarithmic correction.
Entanglement estimators for critical quantum systems show universal scaling laws [Calabrese and Cardy]. Are there equivalance of such scalng laws in classical systems?
It turns out that for classical systems near phase transition, similar universal properties can be found for bipartite information estimators [Calabrese]. At least for mean-field models, along a critical line there is a logarithmic corrections to area law and the coefficient of the logarithm remains constant along the critical line and it is same for a class of models [Cohen, Rittenberg, and Sadhu]. So far our studies are for meanfield models where an exact analytical calculation is tractable.
We want to understand whether such universal laws extend for non-meanfield interactions, as well as along non-equilibrium critical lines.
Other topics.
Some other topics I am interested in are random matrix theory, KPZ-interface growth, fluctuating hydrodynamics, FKPP equation, integrable quantum spin chains, single-file transport, self-organized criticality, and conditioned stochastic processes.
A few relevant publications.
Fractional Brownian motion and field theory.
Large deviations, conditioned stochastic process, hydrodynamic field theory.
Anomalous transport and single-file diffusion.
Pattern formation and self-organized criticality.
A new kind of phase transitions.
Teaching.
TIFR Graduate School course on Advanced Statistical Physics: February - July, 2021
ICTS summer school lectures on Macroscopic Fluctuation Theory: June - July, 2017
Science Notes.
To be updated.
Collaborations.
Some of our past and ongoing collaborations are with the following researchers, in alphabetical order.
Bernard Derrida, College de France
Deepak Dhar, IISER Pune
Shankar Ghosh, TIFR Mumbai
Juliane U Klamser, ESPCI
Satya N Majumdar, LPTMS Orsay
Paul Krapivsky, Boston University
Kirone Mallick, IPhT Saclay
David Mukamel, Wiezmann Institute
Kay J Wiese, ENS Paris
Contact.
If you have any queries related to my research work you may send me an email.