In this page: The problem, Imposing the rules, The number of free variables, Summary

Tips for solving a sample Kakuro

---

The problem and the initial analysis

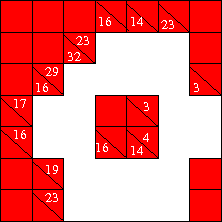
Here is a sample Kakuro problem from Indigo Puzzles. I will show how you solve it step by step. I remind you that rows are labelled by capital letters starting with A for the top row. Columns are labelled by lower case letters, starting with a for the left most column. Each cell is labelled by the row and column: so Aa for the top left cell. The value in cell N is written as [N]. This problem has 22 numbers to be filled in and 16 clues, and therefore apparently 6 free variables. Free variables have to be constrained by applying the rules of the game.

The cells Df, Dg, Ef and Eg are strangely familiar. Since $4=3+1$ and the 3 cannot be put in Eg, it must land in Ef. So we have [Ef]=3, [Eg]=1, [Dg]=2 and [Df]=1. Another part of the puzzle should also be familiar, but we ignore that for the moment. If you wish you could use that already. But in this tutorial I go on now to give names to unknown values, and then use the clues to write others in terms of them as far as possible. This is the process we have called symbolic spreadsheet earlier. Once all the cells have been filled in, we can begin on the hard part of the puzzle: applying the rules.

Integer programming is a name for applying the rules

How many unknowns?

As you can see from the grid alongside, after using all the clues (and solving three of them) we have 6 remaining unknowns. These are $[Bd]=a$, $[Be]=b$, $[Cc]=c$, $[Db]=d$, $[Gd]=f$ and $[Ge]=g$. If the number of unknowns seem excessive to you, put your query on hold for a while. Let's solve the puzzle before we investigate meta-puzzles.

Let's tackle the part that could have been solved by guessing: what is the value of d? We have 3 Type 1 constraints on d: from [Db] we get $1\le d\le 9$, from [Dc] we obtain $8\le d\le 16$ and [Eb] gives us $7\le d\le 15$. Putting them together we have $d=8\; or\; 9$. The Type 2 constraint $[Db]\ne [Eb]$ rules out the value 8 leaving the unique result $d=9$. Having solved this problem the long way round, you can check why it looks familiar. Before going on, take a look at the figure here and check that the value d does not "leak out" of the little 2×2 block of cells, nor does any other unknown value "leak in". This is an example of what we have called a self-contained block. They are useful, because they make up a little piece of the puzzle which can be solved without bothering about the remainder. The two self-contained blocks in this puzzle also contain the unique partitions shown in the left margin, and are therefore especially easy to solve.

Divide and conquer

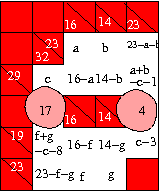
Note another neat thing about self-contained blocks. Both the self-contained blocks in this problem can be replaced by a single cell as far as the algebra is concerned. For the left hand block, this cell holds the value 17 in the column c. For the right hand block it holds the value 4 in the column f. Since this cell is obtained by swallowing up a block, we call it a phagocyte. The value exhibited by a phagocyte need not be a digit. It is obtained by taking the sum of column clues in the block and subtracting from it the sum of the row clues. The blobs in the picture here are the phagocytes which stand in for the collapsed self-contained blocks. See how they reduce the puzzle to something smaller. Faced with a big puzzle, one could just keep collapsing the self-contained blocks, reduce the puzzle to its smallest component and solve it. In this puzzle those are the next steps we work through.

(a,b) and (f,g) are very similiar

The row B and the connected cells Cd, Ce are isomorphic to the row G and the connected cells Fd, Fe. Once we have analysed the constraints due to one of these blocks of 5 cells, the have the same analysis for the other. These blocks of 5 cells are not self-contained: although no outside value leaks in, the values inside do leak out.

The cells [Bd] and [Cd] put two Type 1 constraints on $a$, which together become $7\le a\le 9$. The corresponding constraints on b are $5\le b\le 9$. The Type 1 constraint on [Be] gives $14\le a+b$. The Type 2 in the column d is then $a\ne 8$, and that on column e is $b\ne 7$. There are other Type 2 constraints in row B which are stronger. Let me put them in a table:

[Bd]	[Be]	[Bf]	Status
7	8	8	No
7	9	7	No
9	5	9	No
9	6	8	Possible
9	8	6	Possible

So we have the solution $a=9$ and the two choices $b=6\; or\; 8$. As a result we also have $f=9$ and the choices $g=6\; or\; 8$. The type 2 constraint $[Dc]\ne [Gc]$ then rules out the value 6 for $g$ leaving the unique solution $g=8$. We will see later how the external world of this puzzle fixes $b$.

The end game

The constraints on $c$ are spread out over large parts of the grid. Type 1 constraints in the cells Cc, Ff and Fc together imply $4\le c\le 6$. Type 2 constraints in column f are $c\ne 4\; and\; 6$. Other Type 2 constraints give nothing new, so the unique solution is $c=5$. This gives $[Cf]=3+b$, and reduces the choice of b to the unique value $b=6$.

Since there were 6 unknowns each possibly taking one of 9 values, the solution could have required checking 9⁶ values. We reduced this to checking 4 conditions on d, 7 on a and b together (and a check of 5 values), the same for f and g together, 5 constraints on c and one final one on b and g separately. That is a total of 25 algebraic constraints and 10 explicit checks of pairs of values — a substantial reduction in effort.

Geometry and the number of free variables

We have demonstrated already the apparent mismatch between the number of expected free variables and the actual. This is due to the particular geometry of the problem, which influences the block diagonalization of the linear system with 16 equations and 22 variables. Examine the two 2×2 blocks of cells: one being Db, Dc, Eb and Ec, the other being Df, Dg, Ef and Eg. It is clear that the values of free variables outside these blocks do not enter them, nor do the free variables inside these blocks "leak out". In each of these blocks 4 variables are determined through 3 clues, giving 1 free variable each.

The remainder of the puzzle contains two blocks of 7 cells each, with 4 clues internal to the block and 2 clues to tie the two blocks together. Now, the internal clues leave 3 free variables in each block. Of the 2 remaining clues, only one reduces free variables. The other is a cyclic condition that is identically satisfied along two different paths: [Fc] has the same expression in terms of the free variables shown whether it is computed from the row or column clue. Thus, effectively there is a reduction of the number of clues due to the shape of the grid, leading to an excess number of free variables. This analysis can be made precise by examining the coefficient matrix of the clues. The method of filling formulae into cells simplifies this job: we can call this method a linear algebra spreadsheet.

Summary

So here is what we did. Starting from an empty puzzle we gave a name to one of the variables. Then we propagated it through the puzzle using a method like spreadsheets. Whenever we needed a new symbol, we supplied one, and continued spreadsheeting (or should it be spreading sheet?). Once all the cells were filled we started solving. We first solved the self-contained blocks, then looked at the larger blocks.

To a geek the whole process would look like this. Rewrite the clues as a linear algebra problem: $A.x=c$. Find the kernel of A, then solve the remainder to get $x$_r. To this we can add any vector $x$_n which lies in the null space of A. This computation is faciliated by the symbolic spreadsheet algorithm. Next solve the integer programming problem involving application of the rules of the game to get an unique solution for $x$_n, and thereby of the full puzzle: $x$_r+x_n. Geeks will also know that the second part allows many algorithms, including constraint programming, which is often the method of choice for Su Doku.

---

© Sourendu Gupta. Mail me if you want to reproduce any part of this page. My mailing address is a simple (satisfactory) puzzle for you to solve. Created on 23 November, 2006.