Su Doku Navigation

Su Doku

Su Doku is usually played on a 9 by 9 board, divided into 3 by 3 cells. You can generalize this into playing on an M×M square board broken into non-overlapping rectangular cells, each containing M squares (an obvious question is to how define a puzzle where M is a prime number). The solution of the puzzle is to place M symbols on the board such that each row, column or cell contains each symbol exactly once, without moving the initial clues. Puzzles with M<9 are called Sub Dokus, those for M>9 are called Super Dokus.

Technorati tag:

Related topic: Kakuro

In this page: The puzzle, Counting solutions, Maximum Roku Doku, Minimum Roku Doku, Satisfactory Roku Doku.

Roku Doku

The Mathematics of Su Doku

Roku Doku

The puzzle is set on a six by six board divided into non-overlapping three by two cells. The object is to place the numbers 1 to 6 on the board so that each row, column or cell contains each symbol exactly once. The name comes from "Roku", the Japanese word for 6. Try your hand at some examples of Roku Doku

How many different Roku Doku solutions are possible?

What is the maximum number of clues?

By a general formula the maximum number of clues needed has to be 62-3=33.

Independent clues

A set of clues is called independent if none of them can be derived from the other. (When this set is as large as it can get, then the remainder should be called derivable clues). The general formula above does not apply to independent clues.

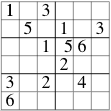
Challenge 1: What is the maximum number of independent clues possible? For Roku Doku the maximum seen to date is 13. An example is given here. Can you do better?

Challenge 2: Count the number of different puzzles for Roku Doku. Two puzzles should be counted as different if the clues are different, even if they lead to the same solution.

What is the minimum number of clues?

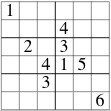
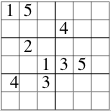
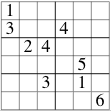
Random enumeration of puzzles seems to lead to the result that at most 9 clues are needed. Shown here are three examples with 9 clues. The last is interesting because it has one cell, one column and one row with no clues, and one of the numbers does not appear in a clue. There are no examples (yet) with 8 clues. This lends credence to the conjecture:
In a M×M Super Doku the minimum number of clues has to be more than M.

Challenge 3: Prove an upper bound on the minimum number of clues for Su Doku or any Super Doku. For that matter, prove the lower bound in the statement above. (For 6×6 grids, 9 clues seems to suffice. For 9×9, standard sudoku, it is claimed that 17 clues are enough.)

Challenge 4: Improve the both the bounds for any Super Doku. The bound in Roku Doku shown above is not a proof. It could help in the general solution if a proof could be produced.

How many satisfactory puzzles?

In the literature on Su Doku one finds references to bifurcation; also called Ariadne's thread, but more commonly known as trial and error. A solution by this means leaves me feeling a little unsatisfied: I am carrying out a set of instructions that any computer can be programmed to execute (the algorithms is known in computer science as depth-first search). So where is the fun which I expected out of solving a puzzle?

Challenge 5: Define "satisfactory" precisely in a sense that a large fraction of Su Doku addicts would agree to. Count the number of satisfactory puzzles. The London Times puzzle claims not to need trial and error: if so the definition of "satisfactory" should encompass all possible puzzles that could be published in this newspaper; ie, the program that generates these puzzles should be provably in the class that you define.

Approaching an answer

A possible answer is that a satisfactory puzzle is one in which there is no need to use trial and error. The three puzzles shown above are examples of satisfactory puzzles in this sense. Is the minimum number of clues the same for all Roku Doku and a satisfactory one? Is there a counting of the number of satisfactory puzzles in this sense?

© Sourendu Gupta. Mail me if you want to reproduce any part of this page. My mailing address is a simple (satisfactory) puzzle for you to solve. Created on 26 September, 2005. Last updated on 28 February, 2006.