How many Two Doku puzzles exist?

The Mathematics of Su Doku

How many Su Doku puzzles exist? This is the biggest unknown about Su Doku now. The challenge is hard, so I will illustrate it here with one of the simplest problems of this kind: Su Doku with 4 cells and two numbers. Call it Two Doku.

Some facts about Two Doku

How many solutions?

The rule is to place two numbers in such a way that no number is repeated in a row or in a column. Two Doku does not have a rule about blocks. A moment's thought will convince you that as soon as you write a number into the upper left corner you can fill in the remainder of the cells. You can write one of two number into the upper left square, so you have two solutions. These are shown above. They each have the symmetry of the coloured square on the right.

Symmetry of the grid

One obvious symmetry of the problem is that the symbols to be filled in are quite arbitrary: Uno or due, Alice or Bob, Deep Purple or Pink Fried. In particular, once you chose the symbols you still have the freedom of permuting them. This is called an S₂ symmetry group: the permutation group of two things. Call this S₂^symb.

The grid itself has some symmetries when it is blank. You could interchange two rows (another permutation symmetry): call this S₂^row. Or you could interchange two columns: call this S₂^col. You could reflect by any of the two diagonals, or you could rotate the square by 90 degrees clockwise or anticlockwise, or by 180 degrees. This is usually called a C₄ symmetry group. There is an inversion symmetry which exchanges every corner with its diagonally opposite one. For Two Doku, all these symmetries together are simply the symmetry group of the square (often called D₄).

The full symmetry of the problem is the direct product S₂^symb × D₄, which is just a complicated way of saying that you can do operations on the grid and the entries separately.

Of course, once you fill up the grid, these two types of operations are not completely indepdentn. Notice that if you flip the symbols 1 and 2 in the first solution, then you get the second one. But this permutation of symbols can be undone by simply rotating the square by 90 degrees rotation (or flipping rows, or columns). The two solutions are therefore related by symmetry.

Orbits, essentially different solutions and little groups

Solutions which are related to each other by a symmetry transformation of the problem are said to be in the same orbit of the group. Since the Two Doku solutions can be flipped into each other by symmetries of the symbols or the grid, this means that the two solutions are in the same orbit. Taking one solution from each orbit gives us all the essentially different solutions. Two Doku has essentially just one solution, since it has only one orbit of solutions. We can choose this to be the first solution.

The little group of a solution is the subgroup of the full group that keeps the solution unchanged. Here is a specification of the little group of Two Doku:

1. An element from S₂^symb followed by an element chosen from S₂^row to undo it.
2. An element from S₂^symb followed by an element chosen from S₂^col to undo it.
3. An element from S₂^row followed by an element chosen from S₂^col to undo it.
4. A rotation by 180 degrees
5. Either of the two reflections about the diagonals.

The puzzle tree

Proper and irreducible puzzles

A proper puzzle is one which has exactly one solution. The completed grid is clearly a proper puzzle, although quite a trivial one. One can keep removing clues from a proper puzzle one by one and checking whether the remaining puzzle is still proper. Everytime you produce a new proper puzzle by this means, write it down and put an arrow pointing to this from the puzzle from which it was produced. An irreducible puzzle is one from which no further proper puzzles can be produced. The graph of all proper puzzles starting from a solution is called a puzzle tree.

One can also have inconsistent puzzles. These are puzzles which violate the rules. For example a two-clue Two Doku in which there is a 1 in both squares in the top row is inconsistent. None of the puzzles in the puzzle tree can be inconsistent, since they are obtained by removing symbols from a consistent solution.

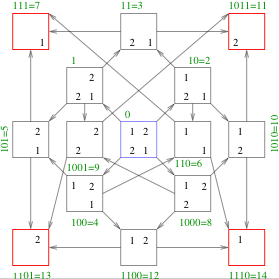
The Two Doku puzzle forest

The collection of puzzle trees starting from each essentially different solution is called a puzzle forest. The Two Doku puzzle forest is a little sparse: it contains only one tree. That one is shown above. Note that every puzzle is proper except the completely empty grid. The irreducible puzzles (outlined in red) are those with exactly one clue. Note that they have no arrows going out of them. They are leaves on the tree.

There are 15 puzzles in all, 4 of which are irreducible. The little group of the solution could have been used to simplify the counting. Puzzles with different numbers of clues cannot be in the same orbit of the little group of the solution. Thus there are is one essentially different puzzle with 4, 3 and 1 clues, and two with 2 clues (two clues in a column or along a diagonal, say).

Note the subtly changed meaning of "essentially different" when applied to puzzles. Applied to solutions, it meant taking one representative solution from each orbit obtained by the action of the full group of symmetries of Two Doku, ie, S₂^symb×D₄. When applied to puzzles, we still mean to take one representative puzzle from each orbit, but the orbit can be constructed by examining only the action of the little group of the solution on the puzzles.

The puzzle hypercube

Here is a representation of the puzzle tree which is very useful for programming its enumeration. Number every square sequentially, first travelling along the top row, then the second and so on. There are M² squares (here 4). While enumerating the tree we ask every square of the solution whether its value remains in the set of clues or not. If the answer is yes, write down a zero for that square, otherwise a one. Call this the skeleton of the puzzle. Then treat the skeleton as a binary number by multiplying the value in the cell by 2^c where c was the numbering of the square, and summing over all squares. The skeleton and its representation as a number is shown in green in the picture of the tree above.

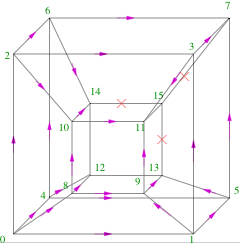
Now, the ordered set of zeroes and ones which comprise the skeleton of the puzzle can be thought of as the coordinates of the corners of a hypercube in M² dimension. For Two Doku this is the usual 4-dimensional hypercube, the tesseract. The identification of puzzles with corners of the cube is shown by the numerical values of the skeleton attached to each corner.

Note that the skeleton 15 is not part of the puzzle tree, since it does not give a proper puzzle. We have indicated this by putting a cross on each link that joins it to another skeleton. On all other links note the direction of the arrow: this always leads from the skeleton with smaller value to that with the larger. If you want to know why, just examine the definition of the value of the skeleton and the reason why it can't be the opposite will become as clear as acid rain.

Symmetries of skeletons and hypercubes

Since the vertices of the hypercube are identified with the skeletons of puzzles, it is clear that the symmetries of the skeletons are subgroups of the symmetries of the hypercube. Why a subgroup? The symmetries of the hypercube obviously consist of any operations which permutes the vertices. However, the symmetries of skeletons do not change the number of ones and zeroes, and therefore keep two of them unchanged— the ones numbered 0 and 2^M2. Therefore, the number of allowed operations on skeletons is smaller, and hence the group must be a subgroup of the symmetries of the hypercube.

The largest such subgroup contains all rotational symmetries about the "body diagonal" which joins the two fixed points of the hypercube, and reflection symmetries in hyperplanes orthogonal to this line. For Two Doku, the allowed rotations interchange (1,2,8,4) cyclically. This allows cyclic interchanges of (7,11,14,13) and (3,10,12,5), but only flips of (6,9) between themselves. Even smaller subgroups of allowed rotations about body diagonals of hypercubes may be allowed for larger Su Dokus.

Maximum and minimum number of clues

Complicated questions about the puzzles, for example the maximum and minimum number of clues among the irreducible puzzles, now reduce to inspecting the puzzle forest. For Two Doku the answer is 1 for each. The total number of proper puzzles is 30, the total number of irreducible puzzles is 8. The number of essentially different proper puzzles is 5, of which one is irreducible. All puzzles are satisfactory.