All known results
The Mathematics of Su Doku
Is there a M×M Super Doku?
A Super Doku grid possible for every M which is non-prime. For M=pq, tile the M×M grid by p×q rectangular cells. The next step is to prove that there is at least one arrangement of M symbols such that each row, column and cell contains one and only one occurrence of each symbol. But this is so easy that I don't show it here.
When M is prime, one can try to tile the grid with any tile made of M squares (call this a tile of area M). This cannot be done with tiles of only one shape. So take the minimum number of shapes of tiles of area M required to tile a M×M grid.
Non-unique grids are also possible whenever a composite M can be factored in two different ways. The smallest non-unique Super Doku grid is for M=12, when one can have 2×6 cells or 4×3 cells. The next is M=16, which can have the regular 4×4 cells or 8×2 cells.
How many different Su Doku solutions are possible?
Here we list the number of possible arrangements of completed puzzles. This is not equal to the number of different puzzles: since different clues may lead to the same completion of the puzzle.
| N | Latin Squares | Su Doku Solutions |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 12 | 6 |
| 4 | 576 | 288 |
| 5 | 161280 | 1680(1) |
| 6 | 812851200 | |
| 7 | 61479419904000 | |
| 8 | 108776032459082956800 | |
| 9 | 5524751496156892842531225600 | 6670903752021072936960 |
Footnotes
- This count is for one specific tiling of the 5×5 grid.
How many different Su Doku puzzles exist?
| M | Puzzles | Irreducible puzzles | Reference |
| 1 | 1 | 1 | |
| 2 | 30 | 8 | Two Doku |
| 4 | 13579680 | 85632 | Shi Doku |
| 6 | Roku Doku | ||
| 8 | |||
| 9 |
Varieties of statements about a puzzle
For every unfilled square in a M×M puzzle one can make M statements such as— "this square contains a 1", or "this square contains a 2", and so on. One can also make M statements which are the negations of these statements: "this square does not contain a 1" etc. The statements which can be checked (provable statements) are interesting as well as the statements which are true.
We give the name elementary statement to either "This square contains the number A" or "This square does not contain the number A". A compound statement is of the form "This square contains one of the numbers in the set Y={Y1,Y2,...} and none in the set N={N1,N2,...}.". A compound statement is self-contradictory if a number appears in both Y and N. The opposite of self-contradictory is consistent.
The number of elements in a set is called its cardinality. If the set is called S, then its cardinality is denoted by C(S). A compound statement which has C(Y)+C(N) > M must be self-contradictory. A compound statement which has C(Y)+C(N) < M and is not self-contradictory is incomplete. A complete and consistent compound statement with C(Y)=1 is a solution of a square.
Proper, inconsistent and incomplete Su Doku
A proper Su Doku is one in which each square has a solution. An inconsistent Su Doku is one in which at least one square is forced to have a complete and consistent compound statement with C(Y)=0 (therefore there is no solution at that square). An incomplete Su Doku is one in which at least one square has a complete and consistent compound statement with C(Y)>1 (therefore more than one solution).
Irreducible Su Doku
A proper Su Doku is reducible when at least one clue can be removed to give another proper Su Doku. An irreducible Su Doku is a proper Su Doku which is not reducible. An irreducible Su Doku becomes incomplete after removing any clue.
Reduction graph for a proper Su Doku
From every proper but reducible Su Doku, one can remove one clue at a time and check whether the corresponding Su Doku remains proper. Draw the starting puzzle as one node in a directed graph, and draw an arrow to every proper puzzle generated by removing a clue. Starting from these nodes, draw arrows again to every proper puzzle obtained by removing one clue. The process must terminate once a set of irreducible Su Dokus are generated. Then we have a directed graph whose root is the original proper Su Doku, each node is a proper Su Doku and the leaves (terminal nodes) are irreducible Su Dokus. This is called a reduction graph.
Counting Su Doku puzzles
Each complete Su Doku solution is a trivial case of a proper Su Doku. Draw the reduction graph for each complete solution. The total number of nodes in all the graphs which are drawn in this fashion is the total number of (proper) Su Doku puzzles. At this time we know next to nothing about reduction trees. So we state two simple questions about them next. Many other questions are also possible. If you have a study of some aspect of the reduction graph, then I would be very interested in hearing from you.
Group theory simplifies the counting a little
Completed Su Doku solutions have a symmetry grid which consists of all permutations of the M numbers and symmetry transformations of the grid. The applications of these transformations can change some of the completed solutions into each other. From each such set, remove all but one solution. The solutions which remain after all such sets are found and one representative from each is retained are called essentially different solutions. The number of essentially different Su Doku solutions is much smaller than the total number of solutions. Since reduction tree contain only proper Su Dokus, and each proper Su Doku has an unique solution, one needs to construct reduction trees only for essentially different solutions. The reduction tree of any other solution can be generated by the action of the group symmetry that relates the root of that tree to the root of its representative.
What is the maximum number of clues?

In a M×M Super Doku, the maximum number of clues which can be filled in and still give an incomplete puzzle is .
The picture above shows a Shi Doku in which 12 clues do not lead to a solution and a 13th is necessary. Extensions to all Su Doku are trivial. Filling in one more clue makes it a proper puzzle. However even the completed grid is a proper puzzle, and clearly M2 is not the answer anyone expects for the maximum number of clues.
Maximum number of clues in an Irreducible Su Doku
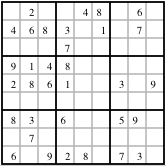
One non-trivial and well-defined question is what is the maximum number of clues in an irreducible Su Doku. By specifying that the puzzle must be irreducible, one gets rid of the irritatingly obvious answer that the maximum number of clues is M2! In the Shi Doku example above, not all clues are independent. The clues marked in red can be removed still leaving exactly the same ambiguity as before. So one more clue added and all the clues in red deleted leave an irreducible puzzle with 6 clues. This happens to be a maximum. The Su Doku example shown here has 33 independent clues and leads to a complete solution. (Example courtesy of Ocean, on the Sudoku Forum).
| N | Maximum clues | Reference |
| 1 | 0 | |
| 2 | 1 | |
| 3 | 2 | Sub Doku 3 |
| 4 | 6 | Shi Doku |
| 5 | 10(1) | Go Doku |
| 6 | ≥13; <33 | Roku Doku |
| 7 | ||
| 8 | ≥29; <61 | Example (?) |
| 9 | ≥33; <78 | Example above |
Footnotes
- This count is for one specific tiling of the 5×5 grid.
All the examples which lead to the conjectures in the table above have been generated by a greedy algorithm with trackback. It is not known whether other ways of generating puzzles succeed in placing a larger number of independent clues.
Counting the number of different puzzles
In the example above, a different set of independent clues would be to take the clues as given in the left two columns, but in the right two columns use the two "E"s instead of the two "R"s. This tells us that two different sets of independent clues can lead to the same solution. Therefore, the counting of the previous section gave the number of solutions, not the number of possible puzzles.
What is the minimum number of clues?
| N | Minimum clues | Reference |
| 1 | 0 | |
| 2 | 1 | |
| 3 | 2 | Sub Doku 3 |
| 4 | 4 | Shi Doku |
| 5 | 4(1) | Go Doku |
| 6 | ≤9 | Roku Doku |
| 7 | ||
| 8 | ||
| 9 | ≤17 | Royle: Minimum Sudoku |
| improved to 17 | McGuire, Tugemann, Civario (2012) |
Footnotes
- This count is for one specific tiling of the 5×5 grid.
The results for and 2 are obvious. The values
for , 4 and 5 are solid. All others are upper bounds, since
a systematic search procedure has not been set up. Here is the only
known theorem about minimum clues:
In a M×M Su Doku the minimum number of clues has to
be at least M-1.
This lower bound is saturated for and 3 (also trivially for
). Can one prove a more precise bound for all M?
How many satisfactory puzzles?
In the literature on Su Doku one finds references to bifurcation; also called Ariadne's thread, but more commonly known as trial and error. A solution by this means leaves me feeling a little unsatisfied: I am carrying out a set of instructions that any computer can be programmed to execute (the algorithms is known in computer science as depth-first search). So where is the fun which I expected out of solving a puzzle?
Challenge 5: Define "satisfactory" precisely in a sense that a large fraction of Su Doku addicts would agree to. Count the number of satisfactory puzzles. The London Times puzzle claims not to need trial and error: if so the definition of "satisfactory" should encompass all possible puzzles that could be published in this newspaper; ie, the program that generates these puzzles should be provably in the class that you define.
Approaching an answer
A possible answer is that a satisfactory puzzle is one in which there is no need to use trial and error. The three minimum Roku Dokus shown (elsewhere) are examples of satisfactory puzzles in this sense. Is the minimum number of clues the same for all Roku Doku and a satisfactory one? Is there a counting of the number of satisfactory puzzles in this sense?
© Sourendu Gupta. Mail me if you want to reproduce any part of this page. My mailing address is a simple (satisfactory) puzzle for you to solve. Created on 26 September, 2005. Last updated on 9 February, 2012.